| Kidney Res Clin Pract > Volume 40(2); 2021 > Article |
|
Abstract
Backgrounds
Methods
Results
Figure 1.
Selection of study participants.
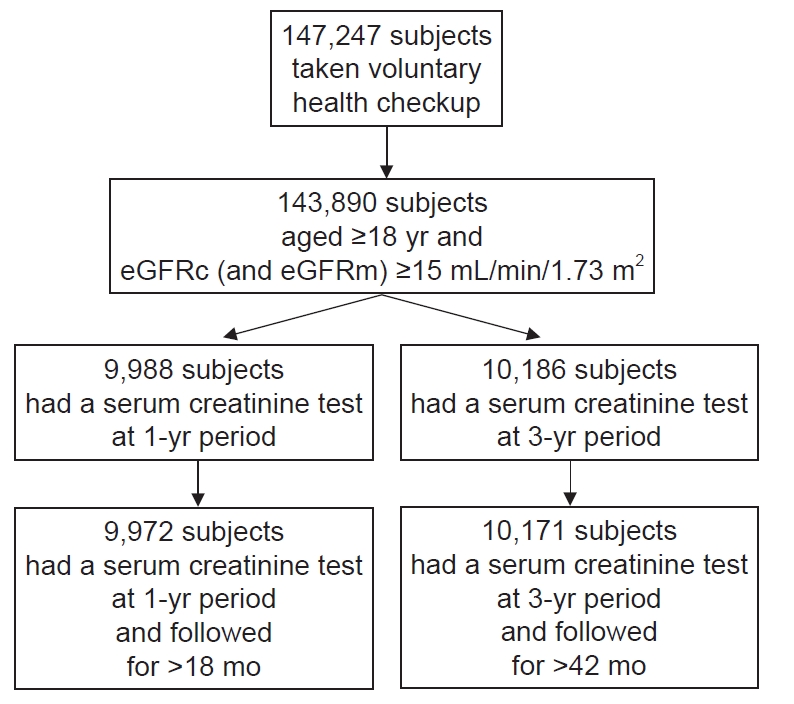
Figure 2.
Receiver operating characteristic curves for changes in eGFR.
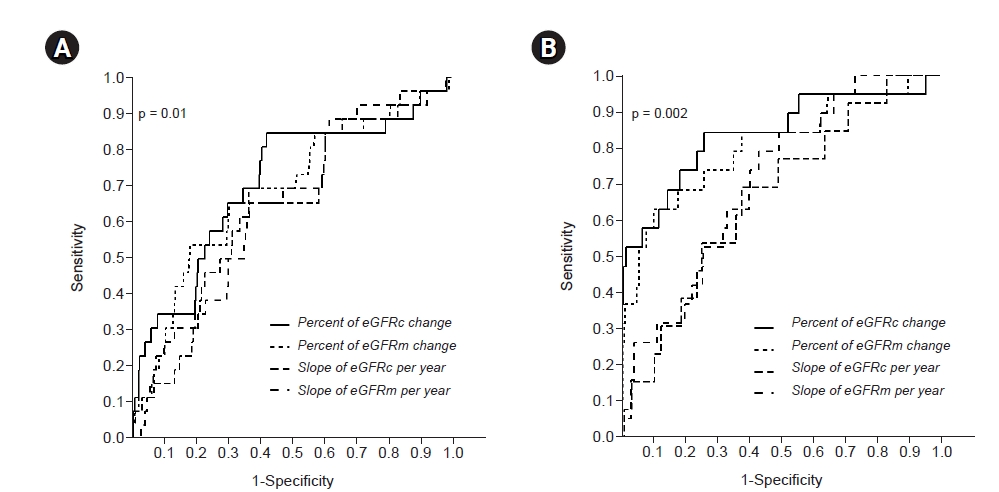
Figure 3.
Adjusted hazard ratio for end-stage renal disease associated with percent change in eGFR.
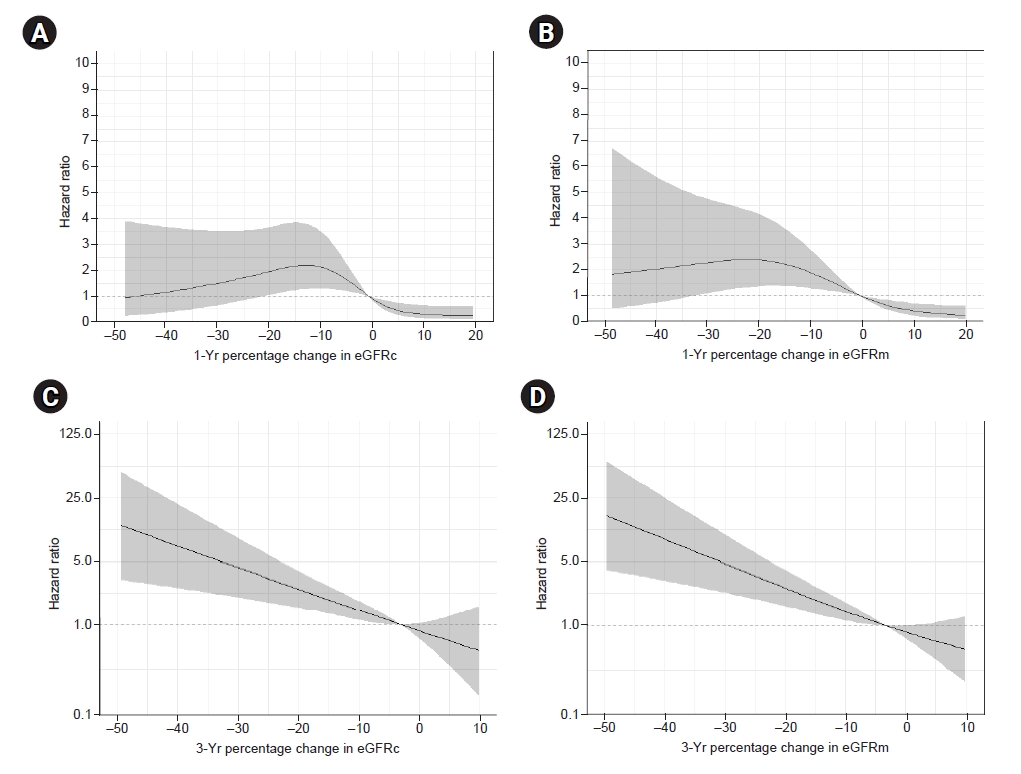
Figure 4.
Adjusted hazard ratio for end-stage renal disease associated with eGFR slope.
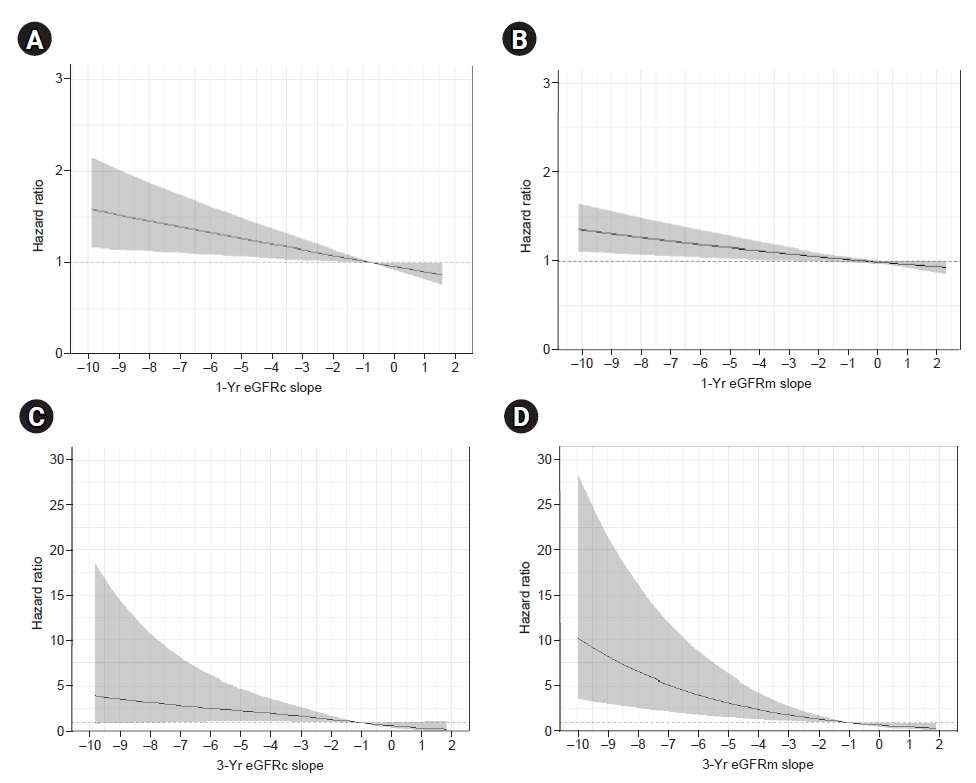
Table 1.
| Variable |
Participant |
p-valuea | |
|---|---|---|---|
| YR1 | YR3 | ||
| No. of patients | 9,972 | 10,171 | |
| Age (yr) | 53.8 ± 11.1 | 53.3 ± 11.2 | 0.004 |
| Male sex | 5,980 (60.0) | 5,998 (59.0) | 0.15 |
| Diabetes mellitus | 1,053 (10.6) | 1,056 (10.4) | 0.98 |
| Hypertension | 2,539 (25.5) | 2,513 (24.7) | 0.25 |
| Body mass index (kg/m2) | 24.0 ± 2.9 | 23.9 ± 2.9 | 0.09 |
| SBP (mmHg) | 121 ± 17 | 120 ± 17 | 0.14 |
| DBP (mmHg) | 75 ± 12 | 75 ± 12 | 0.83 |
| Hemoglobin (g/dL) | 14.6 ± 1.5 | 14.5 ± 1.5 | 0.28 |
| Cholesterol (mg/dL) | 205 ± 36 | 204 ± 36 | 0.32 |
| Triglyceride (mg/dL) | 129 ± 81 | 128 ± 87 | 0.43 |
| HDL-C (mg/dL) | 56 ± 14 | 56 ± 14 | 0.18 |
| Fasting glucose (mg/dL) | 99 ± 24 | 99 ± 24 | 0.48 |
| Protein (g/dL) | 7.4 ± 0.4 | 7.4 ± 0.4 | 0.27 |
| Albumin (g/dL) | 4.4 ± 0.3 | 4.4 ± 0.3 | 0.38 |
| AST (U/L) | 26 ± 15 | 26 ± 18 | 0.59 |
| ALT (U/L) | 29 ± 28 | 29 ± 27 | 0.86 |
| ALP (U/L) | 69 ± 21 | 69 ± 20 | 0.50 |
| Uric acid (mg/dL) | 5.5 ± 1.4 | 5.5 ± 1.5 | 0.69 |
| Calcium (mg/dL) | 9.1 ± 0.5 | 9.1 ± 0.5 | 0.21 |
| Phosphorus (mg/dL) | 3.7 ± 0.8 | 3.7 ± 0.8 | 0.98 |
| eGFRc (mL/min/1.73 m2) | 95.8 ± 15.4 | 95.9 ± 15.4 | 0.39 |
| ≥90 | 6,773 (67.9) | 6,949 (68.3) | |
| <90, ≥60 | 3,024 (30.3) | 3,049 (30.0) | |
| <60, ≥30 | 162 (1.6) | 161 (1.6) | |
| <30 | 13 (0.1) | 12 (0.1) | |
| eGFRm (mL/min/1.73 m2) | 95.4 ± 27.3 | 95.0 ± 25.9 | 0.31 |
| ≥90 | 5,148 (51.6) | 5,233 (51.5) | |
| <90, ≥60 | 4,592 (46.0) | 4,702 (46.2) | |
| <60, ≥30 | 219 (2.2) | 224 (2.2) | |
| <30 | 13 (0.1) | 12 (0.1) | |
| Proteinuria by dipstick | 0.29 | ||
| None or trace | 8,546 (85.7) | 8,832 (87.2) | |
| 1+ | 1,102 (11.1) | 1,010 (10.0) | |
| ≥2+ | 288 (2.9) | 283 (2.8) | |
Data are expressed as number only, mean ± standard deviation, or number (%).
ALP, alkaline phosphatase; ALT, alanine transaminase; AST, aspartate transaminase; DBP, diastolic blood pressure; eGFR, estimated glomerular filtration rate; eGFRc, eGFR by the 2009 Chronic Kidney Disease-Epidemiology Collaboration creatinine equation; eGFRm, eGFR by the modified Modification of Diet in Renal Disease equation; HDL-C, high density lipoprotein cholesterol; SBP, systolic blood pressure; YR1, 1-year eGFR group; YR3, 3-year eGFR group.
Table 2.
AUC, area under the ROC curve; eGFR, estimated glomerular filtration rate; eGFRc, eGFR by the 2009 Chronic Kidney Disease-Epidemiology Collaboration creatinine equation; eGFRm, eGFR by the modified Modification of Diet in Renal Disease equation; ESRD, end-stage renal disease; ROC, receiver operating characteristic; YR1, 1-year eGFR group; YR3, 3-year eGFR group.
Table 3.
Data are expressed as eGFR change (%) or index (95% confidence interval).
DOR, diagnostic odds ratio; eGFR, estimated glomerular filtration rate; eGFRc, eGFR by the 2009 Chronic Kidney Disease-Epidemiology Collaboration creatinine equation; eGFRm, eGFR by the modified Modification of Diet in Renal Disease equation; ESRD, end-stage renal disease; LR (–), negative likelihood ratio; LR (+), positive likelihood ratio; NPV, negative predictive value; PPV, positive predictive value; YR1, 1-year eGFR group; YR3, 3-year eGFR group.
References
- TOOLS
-
METRICS

- ORCID iDs
-
Kipyo Kim

https://orcid.org/0000-0003-4166-1801Eunji Baek

https://orcid.org/0000-0001-9226-7703Suryeong Go

https://orcid.org/0000-0001-8118-7994Hyung-Eun Son

https://orcid.org/0000-0002-8719-3823Ji-Young Ryu

https://orcid.org/0000-0003-4134-1007Yongjin Yi

https://orcid.org/0000-0001-8553-7189Jong Cheol Jeong

https://orcid.org/0000-0003-0301-7644Sejoong Kim

https://orcid.org/0000-0002-7238-9962Ho Jun Chin

https://orcid.org/0000-0002-3710-0190 - Related articles
-
Performance comparison of estimated glomerular filtration rate equations2014 September;33(3)



 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Supplement 1
Supplement 1 Print
Print